Fixation index, or F_ST, is a univariate statistic calculated as the ratio of variance within populations to the variance between populations. Within insect population genetics, F_ST is used to score, and then rank, the correlation between variants and the population structure.

The focus of my Ph.D. dissertation was to investigate variable importance measures as calculated via Random Forests as an alterative to F_ST. I’ve also begun looking at Logistic Regression Ensembles.

In addition to these two machine learning approaches, I wanted to investigate a statistical method, Cramer’s V. Cramer’s V measures the assocation (correlation of unsigned variables) of nominal (categorical) variables. I went ahead and implemented Cramer’s V in the dev branch of my population methods exporation toolkit Asaph.

I used the Burkina Faso An. gambiae and An. coluzzii samples from the Anopheles gambiae 1000 genomes project to compare Cramer’s V and F_ST. I calculated the F_ST scores for each SNP using vcftools. I calculated Cramer’s V using Asaph on data imported using both the counts and categories feature encoding schemes. I then plotted F_ST vs Cramer’s V (counts) and F_ST vs Cramer’s V (categories) to get a sense of the correlation between the two metrics.

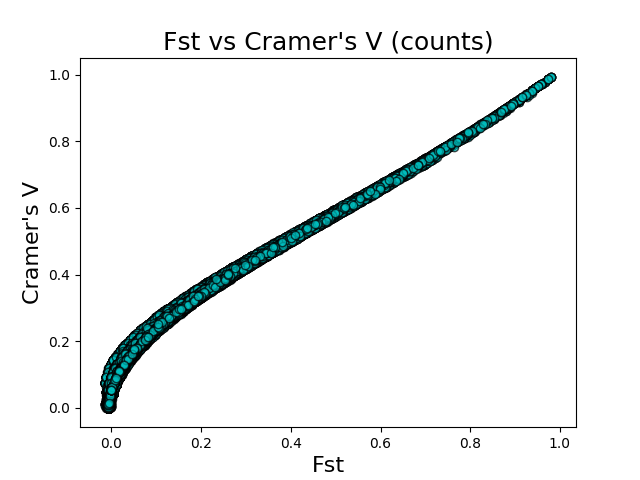
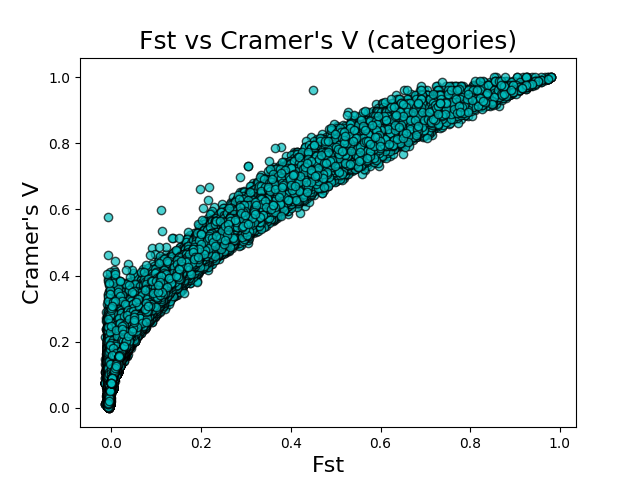
The above figures give the scatter plots of F_ST vs Cramer’s V with the counts and categories feature encodings, respectively. Cramer’s V calculated on the count-encoded features has a \(r^2\) value of 0.865 vs F_ST, while Cramer’s V calculated on the count-encoded features has a \(r^2\) value of 0.818 vs F_ST.

Conclusion

Along with Random Forests and Logistic Regression Ensembles, Cramer’s V is another alternative to F_ST for finding variants that best describe the genetic basis of differences between two populations. Cramer’s V correlates well with F_ST, but a simple correlation analysis doesn’t tell us which metric is more appropriate for a given situation. Substantial work remains to validate the four methods and compare them.